title: 基础算法——搜索.md
toc: true
date: 2021-12-22 09:25:00

基础算法——搜索

January 10, 2021 @KeYuan Liu

本文代码如无特殊说明，全部为伪代码

1. 递归函数

eg：求n的阶乘

int f(int n)
{
    if(n==0)
        return 1;
    return f(n-1)*n;
}

注意 : 在编写一个递归函数时，函数的停止条件是必须的。没有终止条件的递归函数会无休止的运行下去。程序就会失控崩溃了。

接下来，我们想一下斐波那契数列。请读者自己思考一下。其实很简单。

int f(int n)
{
    if(n<=1)
        return n;
  return f(n-1)+f(n-2);
}

可以证明，这个函数的复杂度是$2^n$。指数级别的复杂度是相当之高的。对此，我们要思考，如何简化复杂度。

在f中，如果n是一定的，无论调用多少次，都会得到相同的答案，不如我们尝试把他们用数组存起来，这样就可以计算一次后快速调用，优化之前的算法。

a[n] //记忆化数组用于存结果
int f(int n)
{
    if(n<=1)
        return n;
    if(a[n]!=0)
        return a[n];
    return a[n]=f(n-1)+f(n-2);
}

2. 栈（Stack）

Stack是一种可以支持pop和push两种操作的数据结构。栈是一种先入后出的简单结构。

#include<stack>

stack<int> q;// stack<数据类型> 名称；
int main()
{
    q.push(1);//1
    q.push(2);//1 2
    cout<<q.top();//2
    q.pop();
    cout<<q.top();//1
}

函数的调用过程是通过栈来实现的。因此递归函数的递归过程也可以改成栈上操作。

3. 队列（Queue）

Queue与Stack类似，都支持pop和push两种操作。但是pop的含义不同了。这里的pop是pop最先进来的元素

#include<queue>

queue<int> q; // queue<数据类型> 名称；
int main()
{
    q.push(1);//1
    q.push(2);// 1 2
    q.pop();//2
    q.push(3);//2 3
    cout<<q.front();//2
}

画张图更好的解释以上两种数据结构？（左侧是栈，右侧是队列）

https://i.loli.net/2021/01/10/NzyV2i84fU5w1RM.jpg

介绍完了以上基本内容，接下来就要讲解一下电风扇 （dfs） 蝙蝠衫 （bfs）

4. 深度优先搜索（DFS）

  深度优先搜索，搜索的手段之一。它是从某个状态开始，不断的转移状态直到无法转移，然后退到前一步状态，继续转移到其他状态。直到找到最终的解。（~~时间复杂度巨高，往往是没有更好的办法的办法~~） 。优点是能遍历出所有的状态。

 举个🌰，[数独](https://baike.baidu.com/item/数独/74847?fr=aladdin)大家都玩过吧。首先在一个格子里填入一个合适的数，然后继续向下一个格子里填数直到发现某个格子无解时停止，然后放弃前一个格子选的数字改用其他数字（这就是回溯！）

一直重复这样的操作直到填入的所有数都合法时退出。根据DFS的特点，递归函数是一个不错的选择。

eg：部分和问题

给定整数A1 A2 …. An,判断是否可以从中选出若干个数，使他们的和恰好为k。（1≤n≤20 |An|,|k|≤ 10^8 ）

~思

~考

~时

~间

~！

~！

Solution：

从第一个开始就要决定它是否要被选。复杂度是2^n 。最后决定完n个数的状态时（选或不选）。答案就出来了。

bool dfs(int poi,int sum)//poi 当前的位置，sum 目前的和
{
    if(poi==n) return sum==k;
    if(dfs(poi+1,sum)) return 1;//下一个不选
    if(dfs(poi+1,sum+a[poi])) return 1;//下一个选
    return 0;//无论是否选不选都不能满足sum==k的条件就返回0
}

DFS有时候还是一个比较有用的算法。虽然复杂度很高，但是枚举出所有状态也是很棒的。（其实它悄悄的用了栈的知识）

5. 宽度优先搜索（BFS）

BFS和DFS有很多类似的地方，比如说从某个状态出发可以抵达所有可到达的装态。但也有很多不同的地方（谁叫他是BFS呢）。首先最不相同的是搜索的顺序（俗话说的好，搜索顺序棒，O（n）出答案）

BFS总是优先搜索距离初始状态最近的状态。就像一只网一样。先向外拓展转移一次的状态，然后在从每一个一次状态中转移到第二次状态。 对于一种状态BFS只访问一次所以复杂度大大降低。

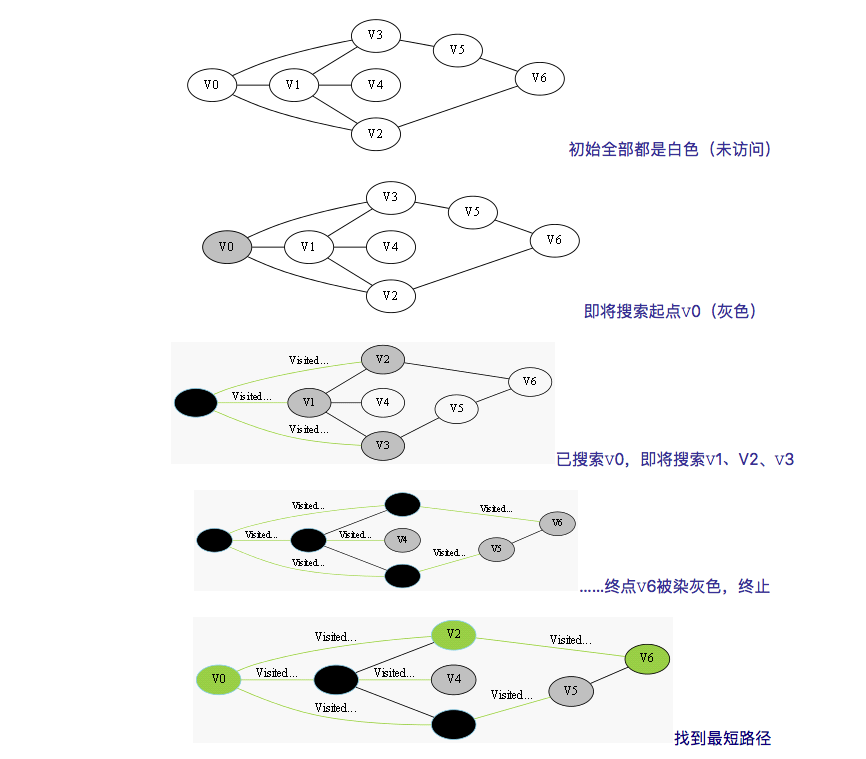
此处我们用队列来解决问题。（先进来的先处理，后进来的后处理）

一般的代码结构是这样的

#include<queue>
queue<int>q;//queue<数据类型> 名称；
void bfs(int x)
{
    q.push(x);
    while(!q.empty())
    {
        int f=q.front();
        q.pop();
        /*
        *此处对f进行操作
        *满足条件的加入队列
        */
    }
}

在求解最短路问题时，bfs的这种思想还是比较有用的。但是状态数和内存空间成正比。而dfs是与最大深度成正比。所以说两种有利有弊吧。

当然搜索不只这些，还有很多高级操作。这里只稍微提及一下剪枝

在dfs过程中，有一些早已明确的知道从当前状态无法转移到合法解。从这种情况下再继续搜索是毫无意义的。不如直接跳过。这种方法就叫做剪枝。

回想一下在dfs中的例题，当sum>k时无论如何都不可能得到答案，所以后面的就没有必要搜索了。

以上就是我所分享的简单搜索。