title: 基础算法——贪心.md
toc: true
date: 2021-12-22 09:25:00
January 15, 2021 @KeYuan Liu
本文如无特殊说明均为伪代码
(notion不支持markdown语法就很😣)
贪心——贪吃,贪睡,贪玩?(此处应有表情包)😂其实当我第一次听到这个名词的时候,我就在想是那个小机灵鬼发明了这个算法。(小孩子才做选择,我全都要!)当然,今天介绍的这个算法确实有那点味。
其实贪心算法就是按照某种规则,不断的选取当前状态下最优策略以达到整体算法的最优解。先来个生活问题热热身。
有1,5,10,100,500元的硬币各n个。现在要用这些硬币支付A元。求最少使用几个硬币?
凭大家的直觉,肯定是尽量的选择面额最大的硬币,因为这样用的数量一定是最少的。然而答案就是这样子的——尽量选择面额最大的硬币。贪心是一种比较高效的算法。他不像上一篇文章所讲的dfs和bfs。贪心过程是一个步步找最优解的过程。相比他俩找出所有状态然后选择自己要那个状态的方案。贪心简直是完美的存在。只有一个状态——最优的状态。
现在让我们考虑下面这个问题(其实也很经典的)
有n个工作,每个工作都从Si开始,在Ti结束。对于每一个工作,你都可以选择参与与否。如果选择了参与,那么自始至终都必须全程参与,而且参与的时间不能重叠(一个时间段内只能干一件事情嘛)。现在勤奋的你想干更多的工作,那么应该如何分配呢?

那我们就来思考了,如何选择才能使干的活最多。不难想到,大家的方案也就以下几种:
但是只有第二个是正确的,下面将举出一些反例。
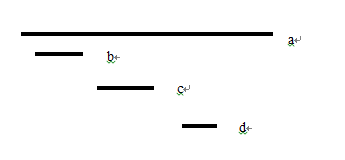
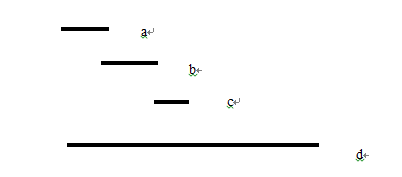
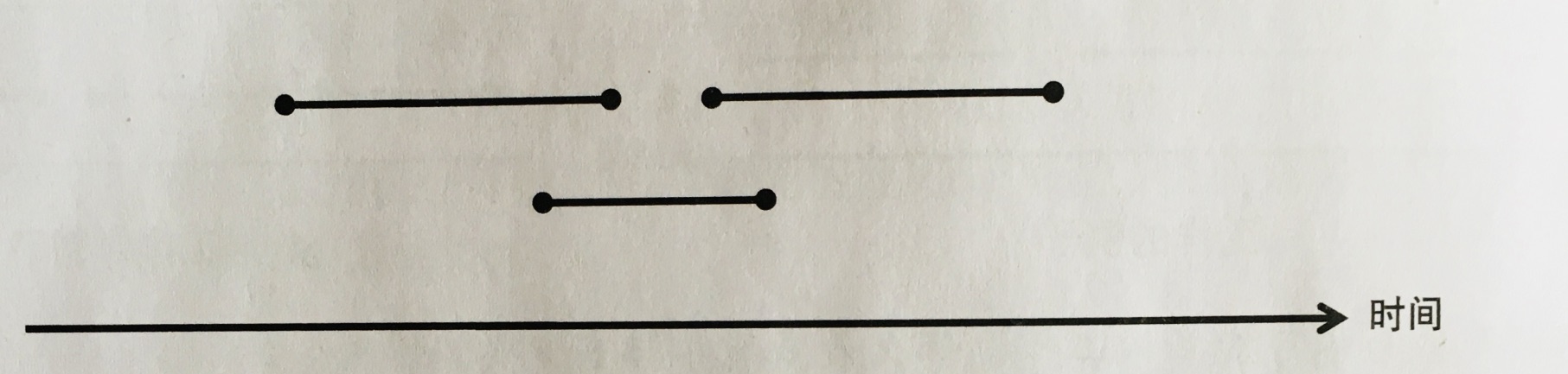
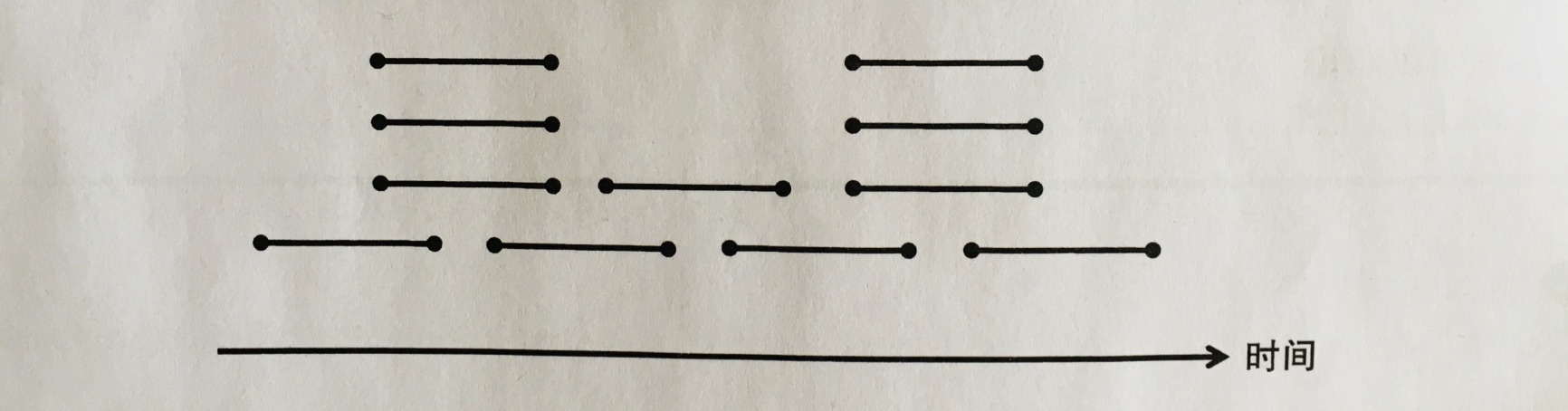
所以说,选择最早结束的是最优选择。这个就是我们贪心的准则。
然后我们在来看一下字典序最小问题
给定一个长度为N的字符串S,要构建一个长度为N的字符串T。起初,T是一个空串,随后反复进行下列任意操作。
目标是构建的字符串T的字典序最小。
举个🌰:
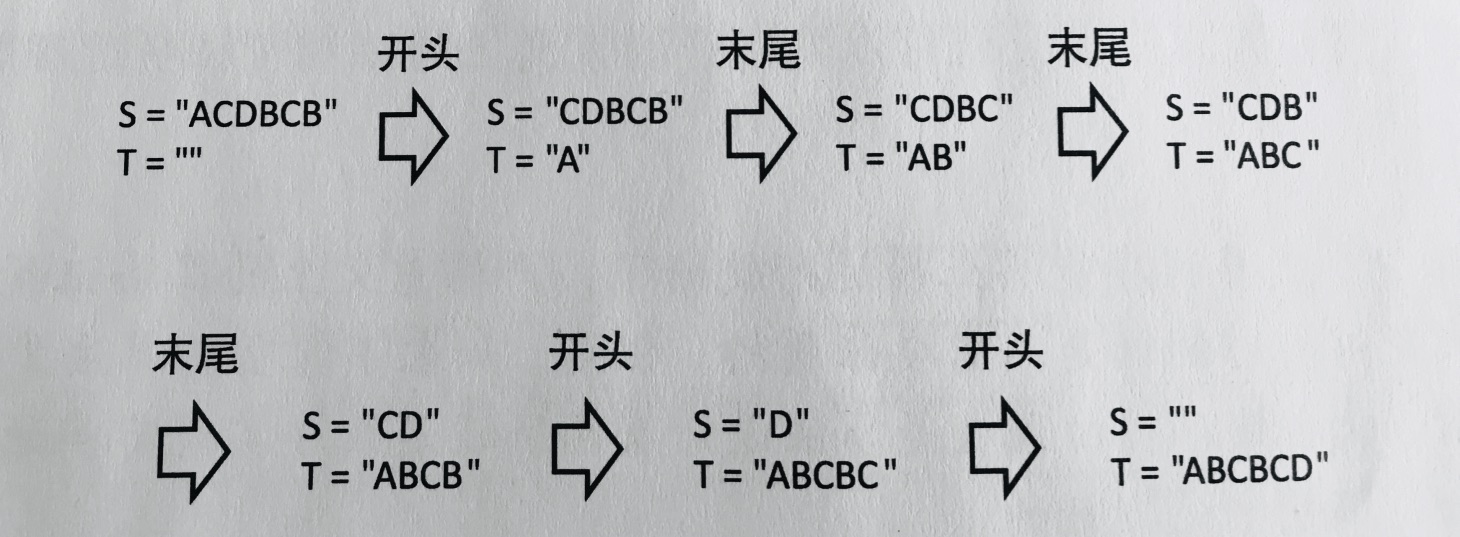
那不难想出,取S的头和尾进行比较,较小的那个放到T的后面,对吧,对吗?不对吧,不全对吧。
如果首尾相同怎么办?这个时候就要用S和S的翻串进行比较。如果S小就用头,如果S大就用尾。如果这个时候还相等怎么办😱??? 那就随便选咯😏。
最后来个简单题练练手。其实贪心的思想有很多,并不全是套路。
直线上有N个点,点i的位置是Xi,从这N个点中选取若干个,给他们加上标记。对于每个点,其距离为R内的区域里必须有一个带标记的点。(自己本身带标记可以认为与其距离为0的位置上有一个带标记的点。)在满足这个条件下,希望为尽可能少的点添加标记,请问至少要有多少点被加上标记呢?
~~~~~~~~~~~~~~~清屏大法好~~~~~~~~~~~~~~~~~~~~~
其实这道题还是蛮简单的,考虑距左端点≤R的最靠右的点,以这个点为起点向右覆盖,每次取向右距离≤R的最靠右的点就好了。
好了,以上就是简单的贪心算法。下一次将在贪心的基础上继续拓展到其他算法。