匈牙利算法
零.前言
匈牙利算法是一个经典的解决二部图最小权值匹配的算法
一.问题描述
匈牙利算法解决的问题一般这样描述:
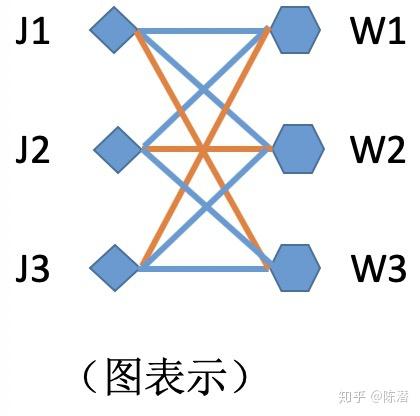
有n个工作,需指派给n个工人,每个工人完成每个工作的时间可能不一样,给出一个算法,使得到的指派结果总的时间最少.
用图表表示:
用矩阵表示:
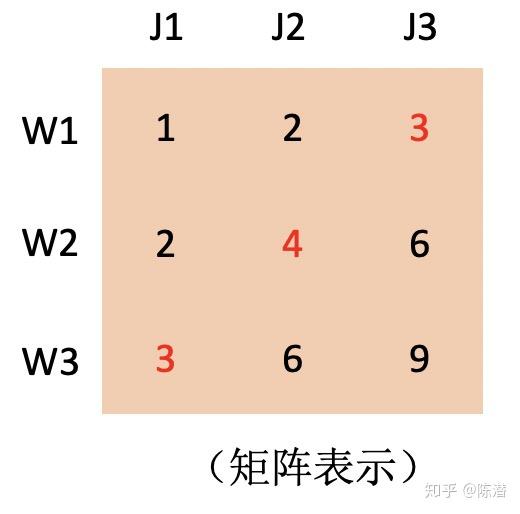
矩阵的(i,j)元素代表第i个工人完成第j的工作的时间,称为权值矩阵
二.算法的步骤
1.找出每一行的最小值并减去最小值
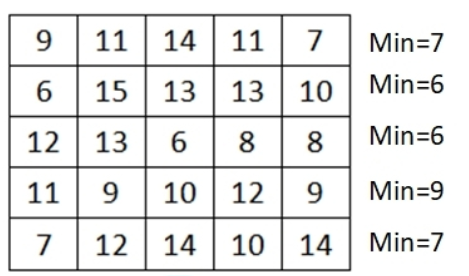
2.减去每一列的最小值
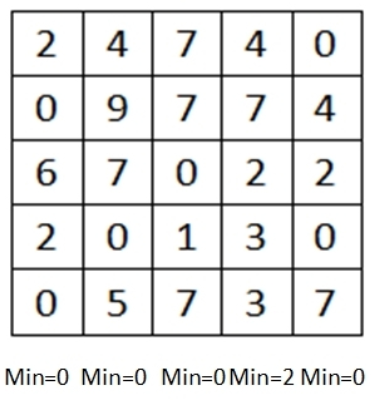
3.做循环:
(1).执行以下步骤覆盖所有零
a.找到含0元素个数最小的行任意标记其中的一个0元素,并对其所在都行列划线

b.重复a直到所有的0都被覆盖(被划掉的0不再参与计数)


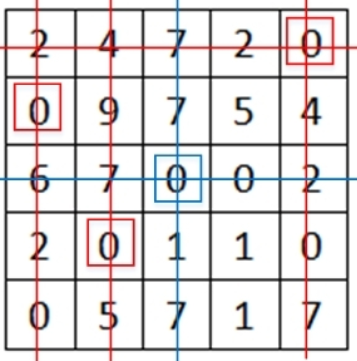
(2).如果被标记的零元素的数量等于矩阵的阶数,中断循环:如果小于矩阵的阶数,继续循环
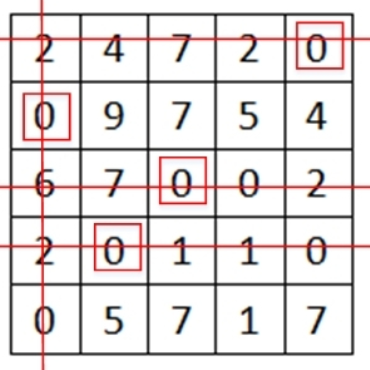
(3).在矩阵中产生更多的零:
a.对没有独立的零元素的行的勾,
对打勾的行所包含零元素的列打勾,
对所有打勾的列中所包含独立零元素的行打勾
b.重复a直至没有勾可打,对打勾的列和没有打勾的行划线(得到了覆盖矩阵中所有零的最小的划线)
c.寻找未被线覆盖的元素中的最小元素K ,所有未被覆盖的元素减去K,划线交叉处的元素加上K,返回循环(1)
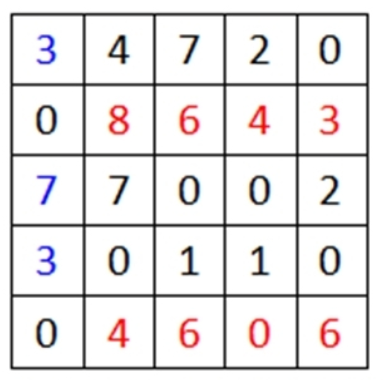
4.被标记的零元素就是最优解
三.扩展:最大匹配
矩阵中的所有元素前面加上符号就可以将最的匹配转换为最小匹配