卡尔曼滤波
学习大纲
前置知识树
- 理解高斯分布
- 理解高斯噪声
- 高斯分布的更新
- 期望的更新
- 方差(协防差矩阵)的更新
- 协防差矩阵的定义
- 高斯分布的乘法—多高斯分布的加权融合
两个基本方程
- 运动方程(预测)
- 观测方程(测量)
预测和测量两者的迭代关联
运动方程的更新
- 期望
- 方差
测量方程的更新
- 转换矩阵H
真实预测信息的融合
- 卡尔曼增益K(融合测量和预测信息)
- 预测信息的期望更新
- 预测信息的方差更新
一.解决问题
结合已知信息优化最优位置,本质是优化估计算法
二.任务本质分析
例子:小车位置的更新


Ft为状态转移矩阵
化为更普通的一般数学形式为

其中,A是状态转移矩阵,B是控制矩阵(控制输入),Wk,Vk为误差(噪声)
卡尔曼滤波本质上是基于观测值和估计值进行综合

其中yk是观测值,y^k是估计值
三.基于观测值进行最优估计
对正态分布x^k和yk进行乘积可以获得最优估计的位置(就像取交集)

用公式表示就是:

其中x^-k是先验估计,x^k是后验估计,Kk是卡尔曼增益
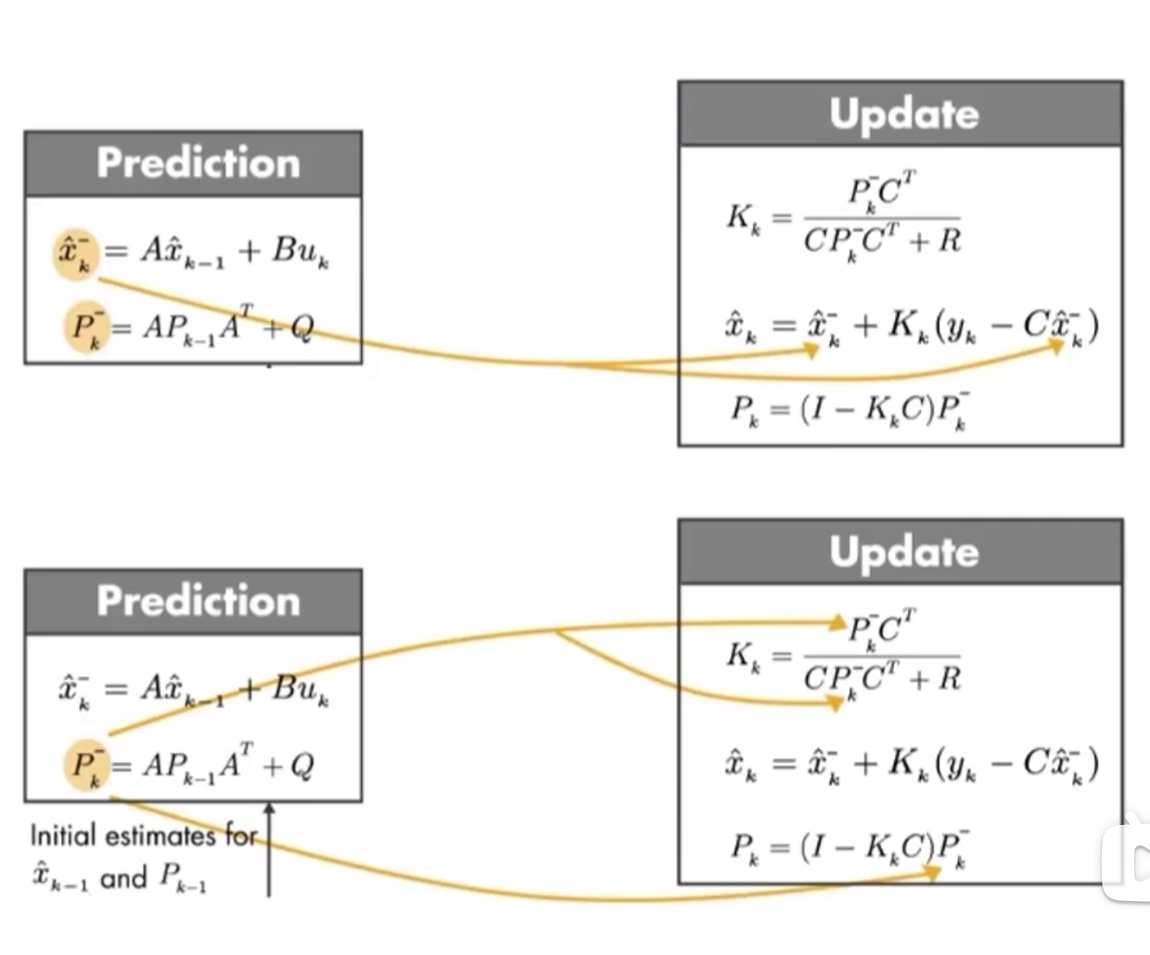
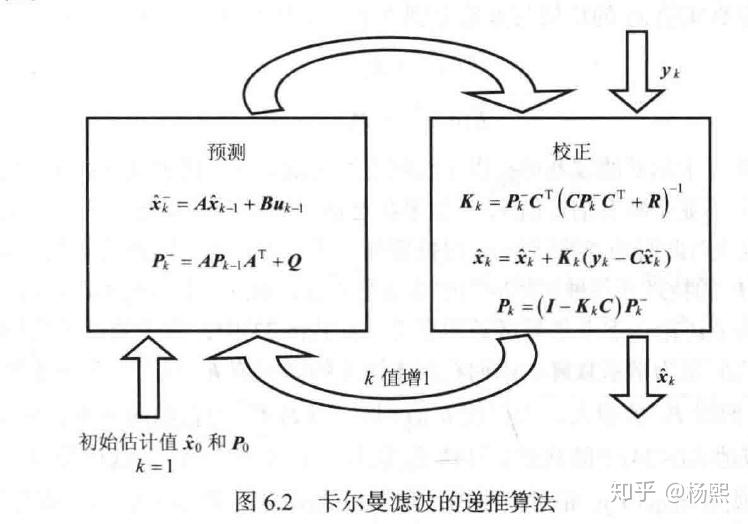
四.预测与更新
卡尔曼滤波包括两大核心模块
1.预测:预测阶段要预测状态和协方差

p-k是协方差矩阵,对角线是方差,非对角线表示的是状态之间的关系(在单状态中,协方差矩阵就是其方差)
Q是噪音矩阵
2.更新:基于预测值更新参数,预测完后需要根据观测值来修正,用修正后的状态去估计下一帧

五.卡尔曼滤波的使用
1.选择状态量,观测量
2.构建方程
3.初始化参数
4.代入公式迭代
5.调节超参数