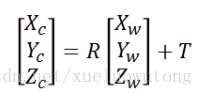像素坐标系到世界坐标系之间的转化
需求
在一张图片里,使用一个像素点的坐标找到,该像素所对应的物体关于相机的相对坐标
已知
1. 像素点在图像中的坐标 x,y
2. 光心到该物体的距离 l
3. 摄像头的焦距 f
4. 图片中的像素点在相机成图的平面内所对应的物理长度,即 dx ,dy
5. 相机的分辨率,即相机所获取的图像的长宽,可计算出u0,v0
6. 相机旋转的角度 和偏移量T
解决方法
在这里主要是用到图片中的世界坐标系、相机坐标系、图像坐标系、像素坐标系
各个坐标系的假设坐标如下图所示:
像素坐标系与图像坐标系的转换
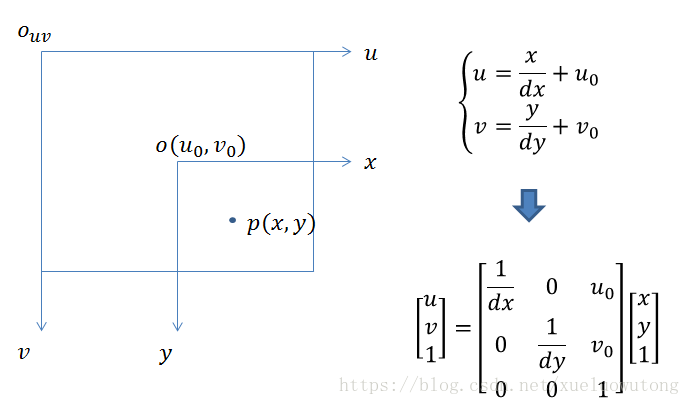
像素坐标系和图像坐标系都在成像平面上,只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点,通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位为mm,属于物理单位,而像素坐标系的单位是pixel,我们平常描述一个像素点都是几行几列。所以这两者之间的转换如下:其中dx和dy表示每一列和每一行分别代表多少mm,即1pixel = dx mm
像素坐标系与图像坐标系坐标之间的关系如下图所示:
将图中的式子转换之后可得:
$$
\begin{bmatrix}
x\
y\
1\
\end{bmatrix}=
\begin{bmatrix}
dx&0&-u_{0}dx\
0&dy&-v_{0}dy\
0&0&1\
\end{bmatrix}
\begin{bmatrix}
u\
v\
1\
\end{bmatrix}
$$
相机坐标系与图像坐标系的转换
在知道目标在图像上的坐标(x,y,f)后,按照已知的距离信息我们可以获得
$$
\frac {x_{c}}{x}=
\frac {y_{c}}{y}=
\frac {z_{c}}{f}=
\frac {l}{\sqrt{x^2+y^2+f^2}}
$$
即:
$$\begin{cases}
x_{c}={\frac{l}{\sqrt{x^2+y^2+f^2}}}x\
y_{c}={\frac{l}{\sqrt{x^2+y^2+f^2}}}y\
z_{c}={\frac{l}{\sqrt{x^2+y^2+f^2}}}f\
\end{cases}
$$
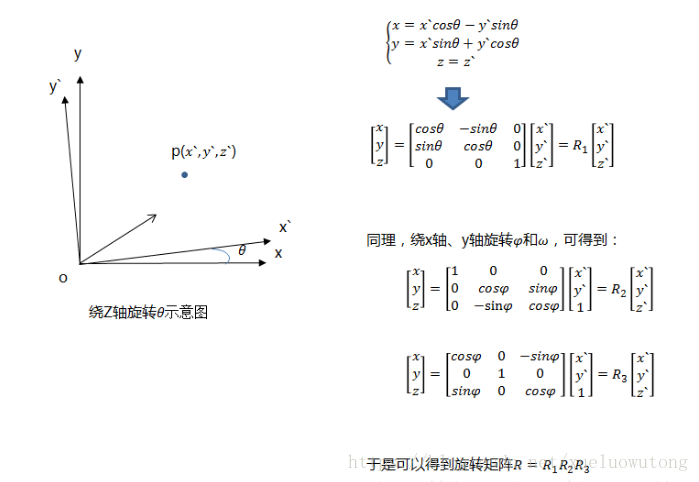
世界坐标系与相机坐标系的转换
从上面两张图,得到
通过转化得到:
$$
\begin{bmatrix}
X_{c}\
Y_{c}\
Z_{c}\
\end{bmatrix}=
\begin{bmatrix}
Cos\theta&-Sin\theta&0\
Sin\theta&Cos\theta&0\
0&0&1\
\end{bmatrix}
\begin{bmatrix}
1&0&0\
0&Cos\varphi&Sin\varphi\
0&-Sin\varphi&Cos\varphi\
\end{bmatrix}
\begin{bmatrix}
Cos\omega&0&-Sin\omega\
0&1&0\
Sin\omega&0&Cos\omega\
\end{bmatrix}
\begin{bmatrix}
X_{w}\
Y_{w}\
Z_{w}\
\end{bmatrix}+T
$$
再得到:
$$
\begin{bmatrix}
X_{w}\
Y_{w}\
Z_{w}\
\end{bmatrix}=
\begin{bmatrix}
Cos\omega&0&-Sin\omega\
0&1&0\
Sin\omega&0&Cos\omega\
\end{bmatrix}^{-1}
\begin{bmatrix}
1&0&0\
0&Cos\varphi&Sin\varphi\
0&-Sin\varphi&Cos\varphi\
\end{bmatrix}^{-1}
\begin{bmatrix}
Cos\theta&-Sin\theta&0\
Sin\theta&Cos\theta&0\
0&0&1\
\end{bmatrix}^{-1}
\begin{bmatrix}
X_{c}\
Y_{c}\
Z_{c}\
\end{bmatrix}-T
$$
最后得到:
$$
\begin{bmatrix}
X_{w}\
Y_{w}\
Z_{w}\
\end{bmatrix}=
\begin{bmatrix}
Cos\omega&0&-Sin\omega\
0&1&0\
Sin\omega&0&Cos\omega\
\end{bmatrix}^{-1}
\begin{bmatrix}
1&0&0\
0&Cos\varphi&Sin\varphi\
0&-Sin\varphi&Cos\varphi\
\end{bmatrix}^{-1}
\begin{bmatrix}
Cos\theta&-Sin\theta&0\
Sin\theta&Cos\theta&0\
0&0&1\
\end{bmatrix}^{-1}
\begin{bmatrix}
{\frac{l}{\sqrt{x^2+y^2+f^2}}}x\
{\frac{l}{\sqrt{x^2+y^2+f^2}}}y\
{\frac{l}{\sqrt{x^2+y^2+f^2}}}f\
\end{bmatrix}-T
$$
转化公式
$$
\begin{bmatrix}
X_{w}\
Y_{w}\
Z_{w}\
\end{bmatrix}=
\begin{bmatrix}
Cos\omega&0&-Sin\omega\
0&1&0\
Sin\omega&0&Cos\omega\
\end{bmatrix}^{-1}
\begin{bmatrix}
1&0&0\
0&Cos\varphi&Sin\varphi\
0&-Sin\varphi&Cos\varphi\
\end{bmatrix}^{-1}
\begin{bmatrix}
Cos\theta&-Sin\theta&0\
Sin\theta&Cos\theta&0\
0&0&1\
\end{bmatrix}^{-1}
\begin{bmatrix}
{\frac{l}{\sqrt{x^2+y^2+f^2}}}x\
{\frac{l}{\sqrt{x^2+y^2+f^2}}}y\
{\frac{l}{\sqrt{x^2+y^2+f^2}}}f\
\end{bmatrix}-T
$$